This page contains much of the documentation that is included
with the iPhone application Maya Date.
 If you received a Mayan date via email, you can read here about
how the Mayan calendars worked, what the various glyphs mean,
and how to read the graphics on your monument.
If you received a Mayan date via email, you can read here about
how the Mayan calendars worked, what the various glyphs mean,
and how to read the graphics on your monument.
If you install the application on your iPhone, you'll be able
to create your own monuments, explore the calendars,
and send new Mayan monuments to friends and relatives.
You can download the application directly from iTunes by
clicking on the App Store button.
Table of Contents
Annual Calendars
In the following pages we'll see how the Mayans counted, how their calendars worked, and how to read a date inscribed in a stone column or monument, called a stele. When you first start this application, you're shown today's date in monument form.
To set the stage, it will help to look at some other calendars. That will help us lock down some of the basic ideas, plus it will give you some insight into features shared by calendars used all over the world.
All human calendars have been influenced by a few measures of time that we're all familiar with from everyday experience. These include the length of a day, the number of days between one full moon and another, and the lengths of the seasons. Perhaps the most important length of time for annual calendars is the solar year, also called the tropical year. This is how long it takes for the Sun to return to any particular location in the sky once it's left that spot. As we know, this takes roughly 365 days.
Before 45 BC, citizens of the Roman empire counted the days with the Roman calendar. This calendar had a length of 355 days, which isn't even close to the length of the solar year. As a result, the calendar was constantly out of synchronization with annual events that were important to the Romans, like the seasonal solstices, which rarely fell on the same day twice. A group of religious leaders tried to fix this problem by inserting extra blocks of days into any year's calendar whenever they felt motivated (apparently bribes and political favors were frequent motivators). Because these changes were unpredictable and varied from year to year, they didn't help solve the problem of creating a reliable, repeating calendar. As a result, nobody was able to keep track of the days with much accuracy.
It took the arrival of Julius Caesar to improve things. In 45 BC he introduced the Julian calendar. This calendar had 12 months, most of which had either 30 or 31 days, for a total of 365 days. The only exception was the second month, which had only 28 days. Every four years one extra day was inserted at the end of that month; each year in which this happened was called a leap year. So over any four-year period, the calendar had an average length of 365.25 days per year, which is very close to, but not quite, the length of the solar year (which is about 365.2423 days). Although this difference seems tiny, it meant that the calendar slipped by about 11 minutes per year, or about 1 day every 130 years.
The Julian calendar got off to a rocky start. For example, for several decades officials misunderstood how leap years worked and added an extra day every 3 years rather than every 4. But eventually these issues got ironed out, and the result was a great improvement over the Roman calendar. But the tiny numerical error we just mentioned slowly added up, and eventually it became too big to ignore. By the 16th century, the Julian calendar was at least 10 days out of synchronization with the Sun. This caused increasing problems with scheduling everything from crop harvests to religious rites and civic functions. The Julian calendar was a lot better than the Roman calendar, but it still wasn't consistent enough. Something had to be done.
In 1582 Pope Gregory XIII introduced the Gregorian calendar. Like the Julian calendar, it has 12 months totaling 365 days. The big advantage of the Gregorian calendar is that it uses a slightly more complicated formula for determining when leap years occur, which keeps it much closer in sync with the Earth's orbit than the Julian calendar. The Gregorian rule is that a year is a leap year if either: (1) it is a multiple of 4 but not 100, or (2) it is a multiple of 400.
This new rule makes just a small tweak in the overall scheme of things, but it gets the average length of a calendar year within about 17 seconds of the length of a solar year. Thanks to this much increased accuracy, the Gregorian calendar is the one that is used by most of the world today.
With precision timekeeping devices like digitally-calibrated telescopes and atomic clocks, today's timekeepers can keep a very precise watch on both the Earth and the calendar. Although we gave a specific value for the solar year above, gravity and other forces cause the Earth's solar year to change a little bit on each orbit. To keep the calendar synchronized to the Earth, an international group of scientists occasionally adds an extra leap minute, or sometimes just some extra leap seconds, at midnight on the last day of June or December.
At about the same time that the Gregorian calendar was introduced, an entirely different calendar was invented. Joseph Scaliger created a calendar he called the Julian Day Calendar. It's an unfortunate name because this calendar has nothing to do with the Julian calendar we discussed above (some people think he named it after his father). In Scaliger's system, the days are simply numbered from 0, starting at some date in the long past. He chose January 1, 4713 BC as his starting point. That date has Julian Date Number 0, written JDN 0. Then the day after it was JDN 1, then JDN 2, and so on. The days add up fast: JDN 2,500,000 will fall on August 31, 2132.
In 1793 the French Republican Calendar was created and adopted in France, and truly embraces the number 10 as used by the metric system. Although the calendar had the usual 12 months, they were divided into 3 weeks of 10 days each. To match the solar year, 5 or 6 extra days were added at the end of the year as needed. Each day was divided into 10 hours, each hour was made up of 100 minutes, and each minute contained 100 seconds. The calendar didn't last long: Napoleon did away with it only a little more than 12 years after it was introduced.
You can find programs online that will convert a date in almost any calendar system into almost any other system. The Roman calendar is not widely used any more, but the Julian calendar is still used in some places. The Julian Day Calendar, and the related Modified Julian Day Calendar, are used today by astronomers and some historians.
There are many other calendars around that are less common than the Gregorian calendar, but still useful. NASA sometimes uses the Truncated Julian Date, which counts the days starting from May 24, 1968. Early IBM PC operating systems used January 1, 1980 as the start of their internal calendar, and the popular Unix operating system counts the seconds starting from January 1, 1970. The iPhone's calendar (which is the same calendar used by all recent Macintosh systems) counts the seconds since midnight on January 1, 2001.
With these basic calendars under our belt, we're ready to look at the Mayan calendars and how they worked.
The Mayan Calendar
Speaking about "The Mayan Calendar" is a little bit tricky, because the Mayans used several calendars at the same time. Depending on how you count, they had 3, 4, 5 or even more calendars all running side-by-side, each one counting off the days independently of the others.
One way to place the Mayan calendar in context is to compare it to the Gregorian calendar. As discussed in the last section, this is the familiar calendar in use in much of the world today. Both the Mayan and Gregorian calendars are based on the idea of cycles. A cycle is just any sequence that repeats over and over. Calendar cycles are usually tied to celestial events like the orbit of the Earth around the Sun, the phases of the Moon, or the changes of the seasons. Every cycle in a calendar works the same way: it steps through its values, and when it gets to the end, it starts over again from the beginning.
The Gregorian calendar is based on two cycles. The first is the weekday cycle, consisting of 7 named days: Monday, Tuesday, and so on. This little 7-day cycle runs all by itself, from Monday to Sunday and then back to Monday, over and over again. It doesn't know anything about months or years: it's just a cycle of seven days, repeating over and over.
The other cycle in the Gregorian calendar is the month cycle. It contains 12 named months, each of which has its own particular number of days. Those days are indicated with numbers, starting with 1. We usually write the month name and the day number side by side, as in 1 January or January 1.
Every day, both the weekday cycle and the month cycle advance independently of each other. Suppose that 1 January (as given by the month cycle) falls on a Tuesday (as given by the weekday cycle). Then the next day, the weekday cycle moves to Wednesday, and the month cycle moves to day number 2 of January. Then they both move again, to Thursday and day 3 of January, and so on.
When the weekday calendar reaches Sunday, it starts again at Monday, regardless of what the month calendar says. When the month calendar reaches 31, the month name advances to February, and the day number goes back to 1. In this way, the month cycle counts the numbered days, and when they reach a particular value the month name advances and the day counter goes back to 1. The weekday cycle just rolls around and around, Monday to Sunday and back again, no matter what is happening with the numbered days and named months.
The Mayan calendar also has independent cycles running at the same time, only they had more of them. This app tracks the three most common Mayan calendars: the 365-day Haab calendar, the 260-day Tzolkin calendar, and the Long Count. Each of these calendars is based on its own sets of cycles. When written together, the Haab and Tzolkin can be considered a single combined calendar called the Calendar Round, which has a cycle of 18,980 days (or 52 years).
(A note on language: in these pages the Mayan words are written using common phonetic versions. Some reference works use more accurate but complex translations. Many of the Mayan words used in the literature and in this application to describe the calendars and their components are neologisms, or new words that were invented to describe these ideas because we don't know what words were used by the Mayans themselves.)
The Haab Calendar
The Mayan calendar called the Haab is roughly similar to the Gregorian calendar. It has 18 named months. Each month is made up of exactly 20 numbered days. The first day of each month is numbered 0, and the last day is day 19. After that, the month name advances by one, and the day goes back to 0.
A calendar made of 18 months of 20 days each is only 360 days long, which is about 5.25 days shy of a full solar year. To get the calendar to more closely match the orbit of the Earth, the Mayans added five extra days after the end of the last month of the Haab calendar. Those extra days aren't considered part of any month - they're like free-floating, independent days. The Mayans thought that these days were bad luck, and they tried hard to avoid doing anything risky on these five days.
The months of Haab, taken in order, are named Pop, Wo, Zip, Zotz, Zek, Xul, Yaxkin, Mol, Chen, Yax, Zak, Keh, Mak, Kankin, Muan, Pax, Kayab, and Kumku. The five days at the end don't belong to any month, but are collectively called Wayeb.
 |
Each day in the Haab calendar is written by simply giving the number of the day followed by the name of the month, as in the Gregorian calendar. Thus the first day is 0 Pop, then 1 Pop, 2 Pop, and so on. The last day of the first month is 19 Pop, so it's followed by the first day of the second month, 0 Wo. After that comes 1 Wo, 2 Wo, and so on. The last named month is Kumku, so the last day of the 360-day calendar is 19 Kumku.
After 19 Kumku come the five free-floating days of Wayeb. Remember that Wayeb is not a month name, but the collective name for these days at the end of the calendar. The first is named 0 Wayeb, which is followed by 1 Wayeb, 2 Wayeb, and so on. Following the last Wayeb day the Haab calendar starts over again, so 4 Wayeb is followed by 0 Pop, and the process restarts for another 365 days.
The Mayans didn't bother to keep track of how many times the Haab calendar rolled around (that is, they didn't count the years as measured by the Haab calendar). That kind of long-term tracking was handled by the Long Count calendar, which we'll discuss below.
The Tzolkin Calendar
The Tzolkin calendar is really two independent calendars running side by side, each based on its own cycle.
The first cycle contains 13 days numbered 1 to 13. This cycle is called the trecena. The other cycle contains 20 named days. Keep in mind that these names don't refer to months, like they do in the Haab or Gregorian calendar. Rather, they're just 20 sequential days with names, like the Gregorian days named Monday, Tuesday, Wednesday, and so on. Each day, both the 13-day cycle of numbers and the 20-day cycle of names each advance by 1.
For comparison with the Gregorian calendar, suppose March 5 of some year fell on a Monday. We would usually write that as "Monday, March 5". But if we know that the month is March, we might leave that off for simplicity's sake, and just write "Monday 5", or "5 Monday." Then the next day would be 6 Tuesday, then 7 Wednesday, and so on. After 11 Sunday, the name cycle (Monday-Sunday) loops back around to the start, but the numbers still have plenty of room to continue. So 11 Sunday would be followed by 12 Monday. Every day the number goes up by one, and the name advances to the next name.
the Tzolkin calendar works the same way. When the 13-day calendar reaches day 13, it "rolls over" so that the next day is day 1, and when the 20-day calendar reaches the 20th named day, it too "rolls over" and the next day takes the name of the first name in the cycle.
The 20 named Tzolkin days, taken in order, are Imix, Ik, Akbal, Kan, Chikchan, Kimi, Manik, Lamat, Muluk, Ok, Chuen, Eb, Ben, Ix, Men, Kib, Kaban, Etznab, Kawak, and Ahau.
 |
Each day is drawn by simply joining the number of the 13-day cycle followed by the name of the day in the 20-day cycle (like writing 5 Wednesday). So starting with 1 Imix, the next day is 2 Ik, then 3 Akbal, 4 Kan, 5 Chikchan, and so on. Finally we get to 13 Ben. The next day, the number cycle goes back to 1, but the name cycle keeps going, so the new day is 1 Ix. Then come 2 Men, 3 Kib, and so on, to 7 Ahau. Now the 20-day name cycle goes back to its start, but the 13-day number cycle is still in the middle so it just keeps going; the next day is 8 Imix, then 9 Ik, and so on.
If you write it all out it takes 260 days for the Tzolkin calendar to make it back to its starting point at 1 Imix. It is not known what name the Mayans used for this period, if they had a name for it at all, but the Aztecs called it a tonalamatl.
Like the Haab calendar, the Mayans didn't bother to number the years of the Tzolkin calendar.
The Lords of the Night
Every day is associated with a creature known as a Lord of the Night. There are nine Lords, and they take turns watching over the days in order, creating a 9-day cycle.
Although we have examples of the drawings used to represent each of the Lords of the Night, their names have been lost. Scholars call them simply G1 through G9.
The nine-day cycle of the Lord of the Night calendar runs around and around, from G1 to G9 and back to G1, independently of what's happening in the other calendars.
 |
The Long Count
The Long Count is really just a way of writing the number of days that have gone by since a particular date thousands of years ago. That starting date isn't when the calendar was first used, but rather is just the day from which all the other days are counted. Traditionally, this date is called the "date of creation", but it's not clear that the Mayans actually meant that to be interpreted as the date that the universe started. All we can really say is that it was used as the starting point for their calendar, just as January 1 of the year 1 was the starting point for the Gregorian calendar.
Since the days are numbered from the date of creation, we could write any particular date as a single big number, just as in the Julian Date Calendar discussed earlier. And in fact this application gives that number to you. But the Mayans didn't write it that way. Their style of writing the Long Count was influenced by the fact that they preferred to think of their numbers in terms of multiples of 20, rather than multiples of 10 as we usually do today.
To get a feeling for this, think about the odometer on a brand-new car. Ignoring any fractions, the odometer shows you a series of digits that tell you how many miles you've traveled. For now, let's suppose that the odometer has just five digits When we write them, we'll put a dash between each digit. So if the odometer reads 0-0-3-4-7, that means you've traveled 347 miles.
Suppose you've picked up your car at the factory. The first time you start it up, the odometer reads 0-0-0-0-0. As you drive, the rightmost digit increases by 1 for each mile you've traveled. After nine miles it reads 0-0-0-0-9. What happens when you keep driving? Of course, the rightmost digit wants to increase, but there's nowhere to go above 9. So that digit wraps around back to its starting point at 0, and simultaneously increases the digit to its left, giving us 0-0-0-1-0. That 1 represents how many 10's of miles you've traveled. When the odometer later reads 0-0-0-2-0, that number 2 tells you that you've traveled 2 chunks of 10 miles each, or 20 miles.
You know what's coming next. After 99 miles, the odometer reads 0-0-0-9-9. After the next mile, the 1's digit rolls around from 9 to 0, pushing up the 10's digit, which also rolls around from 9 to 0, pushing up the digit to its left from 0 to 1. The result is 0-0-1-0-0. The 1 in the third slot tells us how many hundreds of miles the car has gone.
So you can think of the odometer this way: to find the total number of miles, multiply each digit by the number of miles associated with its slot. The rightmost slot represents single miles, the one to its left 10 miles, then 100, then 1000, and so, going up by a factor of 10 every time. So when the odometer reads 5-3-1-2-6, that means we should add (5*10,000) + (3*1,000) + (1*100) + (2*10) + 6. The total is of course just 53,126.
The Mayan Long Count works in just this way. But instead of using the values 0-9 for each digit, they used 0-19 for most of them (but not all, as we'll see). And the first five slots don't represent chunks of 1, 10, 100, 1000, and 10,000 miles (as on the odometer), but instead they represent chunks of 1, 20, 360, 7,200 and 144,000 days (yes, those numbers are weird; in a moment we'll see where they came from). The Long Count is written with periods between each value. Typically, we write only the rightmost 5 digits of the Long Count when we name a date (we'll see why later on). So the very first day of the Long Count calendar would be written 0.0.0.0.0.
Day 2 of the calendar is written 0.0.0.0.1, then 0.0.0.0.2, and so on. When we reach 0.0.0.0.9, we just keep going, because the rightmost slot shows the numbers 0 to 19, so day 11 is written 0.0.0.0.10, then 0.0.0.0.11, and so on. The 20th day is written 0.0.0.0.19. What comes next? The 19 rolls over back to zero, and it bumps up the digit to its left. So the next day is 0.0.0.0.1.0. Now that 1 is telling us how many sets of 20 days have passed. A Long Count of 0.0.0.11.14 represents a day that is (11*20)+14 days since the start of the calendar, or the 234th day.
Now comes a little twist. You might expect that all the slots would run from 0 to 19, just as the car odometer's slots all ran from 0 to 9. But the Mayans wanted the last couple of slots to wrap around close to the end of a year. They noticed that after the rightmost digit (which has 20 values) wrapped around 18 times, that was a total of 360 days, which is close to 365. So the second slot only has 18 values (numbered 0 to 17).
Let's return to the Long Count in the earliest days of the calendar. After 0.0.0.1.0 (the 20th day), we have 0.0.0.1.1, then 0.0.0.1.2, and so on. Then 0.0.0.1.19 is followed by 0.0.0.2.0, and it keeps going. Finally we get to day number 359, with Long Count 0.0.0.17.19. The next day, the rightmost value wraps around from 19 to 0, and it tells the number to its left to go up by one. But since 17 is as high as that slot goes, it too wraps back around to 0 and increments the slot to its own left, resulting in 0.0.1.0.0. That's day number 360. So the 1 in the third position tells us how many sets of 360 days have gone by.
As an example, a Long Count of 0.0.5.4.6 tells us that it is (5*360)+(4*20)+6 days from the start of the calendar (if you multiply that out, you find that this is day 1,886).
The next two slots of the calendar represent multiples of 20 of the slot to their right. So putting it all together, the first slot represents how many chunks of 1 day have passed, the next slots counts chunks of 20 days, then 360 days, then 7,200 days (that's 20*360) and then 144,000 days (20*7,200). The values of the slots go up fast!
The Mayans gave a name to each slot in the Long Count. Working our way from right to left, the 1's location is called the kin, then there's the uinal, tun, katun, and baktun. In addition to a name, each of these slots had its own glyph, or picture. When you read a Long Count date you'll see the picture for each of these slots next to a number that tells you how many times to multiply its value.
Here are glyphs corresponding to the Long Count slots: |
Some scholars believe that the baktun slot (telling us how many chunks of 144,000 days have passed) does not run from 0 to 19 like most of the others, but only from 0 to 12. When it wants to increment from 12, it goes back to 0 and bumps up the number to its left. That slot is called piktun and represents 20*144,000 or 1,872,000 days.
What's the largest date we can write with just the rightmost 5 digits? The kin, tun, and katun slots all run from 0 to 19. The uinal slot runs from 0 to 17. For the moment, let's assume that the baktun only runs from 0 to 12. With that assumption, the biggest date we can write with just five values is 12.19.19.17.19.
Using the GMT1 correlation constant (see the discussion on the next page for details), the date 12.19.19.17.19 falls on 20 December, 2012. This is day number 1,871,199 of the Long Count. The next day everything rolls over, like when your car goes from 9999 to 10,000 miles. The 19 in the kin slot wraps from 19 to 0, which bumps the uinal value to its left, which wraps to 0, bumping the tun, which wraps to 0, bumping the katun, which wraps to 0, bumping the baktun, which wraps to 0, bumping the piktun, which advances from 0 to 1.
So the next day, 21 December 2012, would require us to include the piktun digit, and we'd write 1.0.0.0.0.0. This is day 1,872,000 of the Long Count, so under this assumption piktun slot represents chunks of 1,872,000 days.
On the other hand, the Mayans might have meant the baktun slot to run through the 20 values 0 to 19, like most of the others. If so, the largest date we can write with five values is 19.19.19.17.19, which falls on 12 October 4772. This is day number 2,879,999 of the Long Count. As in the previous discussion, the next day causes everything to roll over to 1.0.0.0.0.0, which is 13 October 4772. This is day 2,880,000 of the Long Count, so under this assumption the piktun slot represents chunks of 2,880,000 days.
There is no conclusive evidence to settle whether the baktun slot rolls over at 12 or 19, and some scholars consider the issue unresolved. Experts will continue to gather and analyze the evidence and debate its interpretation in the hopes of finding a definitive answer. At the moment, the consensus is that the baktun probably rolls over after 12, so that's what's used in this application.
Even after the baktun slot has rolled over, we don't always have to include the piktun value if everyone knows roughly the era under discussion. In the Gregorian calendar we sometimes speak of "the 60's" or "the 90's" without writing the century digits 19 in front of them. The traditional 5-digit Long Count is still useful in the same way. If you share the Long Count date of an event with a friend and you don't include the piktun digit, your friend will probably be able to figure out whether you meant it to be a 0 or 1, depending on whether the event is happening around now, or belongs to the distant past or far-off future.
Assuming the baktun slot rolls over at 12, then including the piktun slot allows us to identify about 37 million days. That's about 100,000 years. With the GMT1 correlation constant, the largest six-value day is 19.12.19.19.17.19. That's 5 November in the year 99,394. Now that will be a good day to have a party!
The Mayans took the long view of time, and named several more slots beyond piktun. They are called (in increasing order) kalabun, kinchiltun, and alautun. Even when those three additional slots have rolled over (about 816 million years from now), you can of course keep adding extra slots as needed, even though they don't have special names. Each one represents a factor of 20 chunks of the slot to its right.
In this app, you may only select Gregorian dates that have valid Long Count counterparts. Thus you can't choose a day before Long Count 0.0.0.0.0.0, or after Long Count 19.12.19.19.17.19. The date picker always allows you to enter all rightmost six digits of a Long Count. If you'd prefer to see the date displayed with a more traditional 5-element Long Count, turn off the "Show Piktun" switch on the Settings tab.
Correlation Constants
The Long Count, as its name suggests, counts off the days since the day 0.0.0.0.0, or "day of creation". What would we call that day in the Gregorian calendar? This is a historian's question that may never be resolved with complete certainty. The quest to determine this starting date is called the correlation problem.
Many scholars have invested significant time and energy trying to figure out what date Long Count 0.0.0.0.0 represents, and there are many theories. To identify a particular solution to the correlation problem, you need only state the Julian Day Number (or JDN) that you want to associate with 0.0.0.0.0 (recall from before that a JDN is simply the index of a given day, counting forward from 1 January, 4713 BC). Most of the theories have JDN values around 580,000. The JDN number you use to set the starting date for the Long Count is called the correlation constant.
The most commonly-accepted theory for the beginning of the Long Count was developed by Joseph Goodman, Juan Martinez, and J. Eric Thompson. Their work, developed over the course of about 50 years from 1887 to 1937, narrowed down the starting date to one of three choices. These correlation constants are now called GMT1, GMT2, and GMT3 after the names of the three men:
- GMT1
- 11 August 3114 BC (JDN 584,283)
- GMT2
- 12 August 3114 BC (JDN 584,284)
- GMT3
- 13 August 3114 BC (JDN 584,285)
The scholarly consensus is that either GMT1 or GMT3 is probably the "right" starting date for the long count. Conventionally, GMT1 is used by most people these days, and that's the value this application uses by default. You can pick one of the other constants, or even specify your own, from the Settings tab.
Because the Gregorian calendar was established in the 16th century, talking about Gregorian dates before then is something of a stretch, because the calendar didn't exist yet. We can, of course, simply extend the calendar backwards, including leap years where the rules tell us they would have gone. This extension of the Gregorian calendar into the past is called the proleptic Gregorian Calendar. You can create a proleptic version of any calendar by running it backwards in this way.
One thing we do know is that on 0.0.0.0.0, the Haab and Tzolkin calendars were not also at their starting points. Rather, on the day of creation, the Tzolkin calendar was at 4 Ahau (the 121st day of its 260-day cycle), and the Haab calendar was at 8 Kumku (the 349th day of its 365-day cycle). The Lord of the Night for this first day was G1.
The Numbers
Mayan counting uses bars and circles. Each circle is worth 1, and each bar is worth 5. In the calendar, typically the bars and circles are drawn vertically. The circles go on the far left, and any bars appear to their right.
So if there are, say, three circles and no bars to the left of a picture glyph, then that represents the number 3. If there are three circles and one vertical bar, then that's the number 3+5=8. Two circles and three bars represents 2+(3*5)=17.
The Mayan number system included the idea of zero. A zero was represented with a tall thin picture about the width of two bars, frequently decorated with internal designs.
 |
The Glyphs
The Mayans used a beautiful and creative system of pictures for their written language. Each symbol is often called a glyph. Each of the Long Count digits has its own glyph, as do each of the Lords of the Night, the 20 named days of the Tzolkin calendar, and the 18 months of the Haab calendar.
With the exception of the Lords of the Night, each glyph in the Mayan calendars is paired with a number. The circles and bars for that number are drawn to the left of the glyph, typically touching its left edge. So for example to identify the 3rd day of the Haab month of Pop, you'd draw the glyph for Pop, and on its left side draw three circles to represent the number 3. Similarly, a Tzolkin day of 13 Lamat would be written by drawing the glyph for Lamat and placing the number 13 (that is, 3 circles and 2 bars) to its left.
The Long Count is given one slot at a time, each attached to the glyph associated with that slot. So if the value in the katun slot is 7, for example, you'd draw the katun glyph and to its left a single bar and two circles for the number 7. In a full Long Count you'd have five (or six) glyphs, one for each slot, each with a number attached to it to tell you how many times to multiply the number of days associated with that slot.
The Lords of the Night each have their own glyph, so there's no need for a number.
In the Roman alphabet, we enjoy an enormous variety of letter forms that are still recognizable (just look at any online font site to see a seemingly endless number of variations on every letter of the alphabet). In the same way, the Mayans often varied their glyphs in creative and artistic ways. The glyphs used in this application were drawn specifically for this program, based on a wide range of historical and scholarly resources.
How To Read A Date
On the main screen, the date is shown in stele form, as it might have been carved in a monument. The figure below shows the layout. If you're not displaying the piktun slot, then the top row is fully spanned by a sign called the Initial Series Introductory Glyph (or ISIG), which announces that the date written below is important.
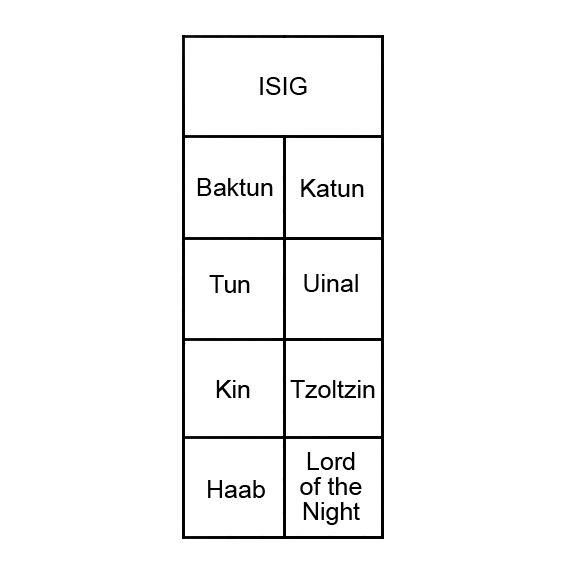 |
Below the ISIG, the five digits of the Long Count appear in order, arranged left to right, top-down. Each digit is formed by joining the glyph for that slot with the bars and dots corresponding to the value in that slot. The baktun and katun are in the first row under the ISIG, then the tun and uinal, and then the kin.
To the right of the kin in the fourth row is the Tzolkin date. On the bottommost row are the Haab date and the Lord of the Night.If you choose to display 6 digits of the Long Count, then the ISIG appears only in the upper-left corner, and the leftmost slot of the Long Count (the piktun) is shown to its right, as in the figure below.
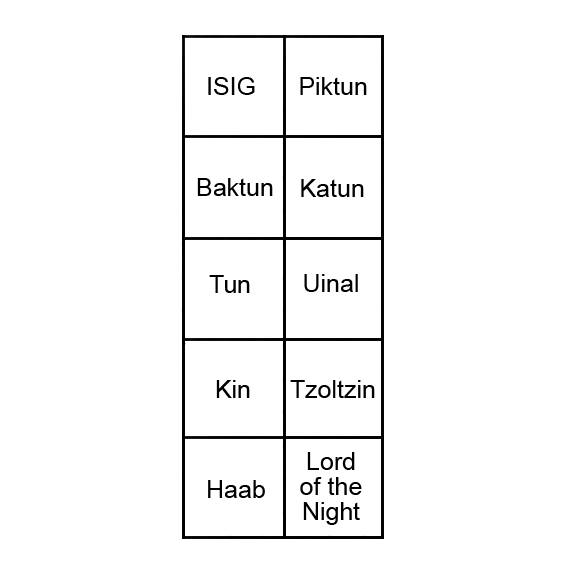 |
On the date-picking screen, the five (or six) digits of the Long Count are drawn left-to-right on the top row. The Tzolkin and Haab dates, and the Lord of the Night, are arranged left-to-right beneath them.
On the main Stele tab, the calendars are shown as described above. The top line of text identifies the Gregorian day. Under that appears the Long Count, followed by the day number (that is, the number of days that have passed since 0.0.0.0.0, or the day of creation). This number is just a more familiar version of the number represented by the Long Count. The next line presents the Calendar Round: the Tzolkin and Haab dates, one after the other. Finally the Lord of the Night is identified by its name (G1 to G9).
More Information
These notes have barely scratched the surface of the Mayan calendar system, and of course haven't touched on any other aspects of Mayan history or culture. Our aim here was to provide a general overview, rather than a deep discussion. You can find out much, much more about the Mayans, their calendars, their language and culture and whatever else interests you by searching online, or visiting your local library.
Many of the reference materials that you can find online and in print are the work of serious amateur and professional scholars. These works contain reliable information that is firmly grounded in both physical and cultural artifacts and the historical record. But as with any subject that is open to interpretation, you can also find plenty of material that is less reliable, building on ideas that may have little to no basis in reality. As always, it's important to read critically, consult the references, and determine for yourself how much to rely on the authority of each source.
If you'd like to learn more about the Mayan calendar system, here are a few places to start that are as close as your nearest library or web browser.
The Wikipedia offers a wide variety of information about all kinds of calendars and calendar systems, and about Mayan culture and history. Many of these articles are well-researched and contain a wealth of additional references if you want to explore any topic in more detail.
An organized collection of hundreds of Mayan glyphs, some with multiple variations, is available in the book Dictionary of Mayan Hieroglyphics by John Montgomery.
Two monographs from the early 1900's are widely considered the definitive descriptions of the Mayan calendar system. Drawings and photographs of stellae, and a discussion of how to interpret the dates that appear on them, appear in Mayan Calendar Systems by Cyrus Thomas, published in the Nineteenth Annual Report of the US Bureau of American Ethnology, 1901. The Mayan calendar system is also discussed and illustrated in detail in An Introduction to the Study of the Maya Hieroglyphs by Sylvanus Griswold Morley, published by the Smithsonian Institution's Bureau of American Ethnology (Bulletin 57), 1915. Both the Thomas and Morley monographs are available in scanned-in form online.
All original artwork and text in this application and on this page are copyright © 2009 Coyote Wind Studios, http://www.coyote-wind.com. If you'd like to use any of our text or graphics, please for permission first.